[Sixth in a series. The beginning is here]
Not your first choice of activity for a sunny afternoon?
As I move you gently as I can through some technical details, be aware that government employees with HUGE computers paid for by YOU are making these same sorts of calculations. They have answers (likely WRONG answers for you) to these calculations when they approach you with “Hi! I am from the government, and I am here to help!!” Do you really want to be unarmed when that happens?
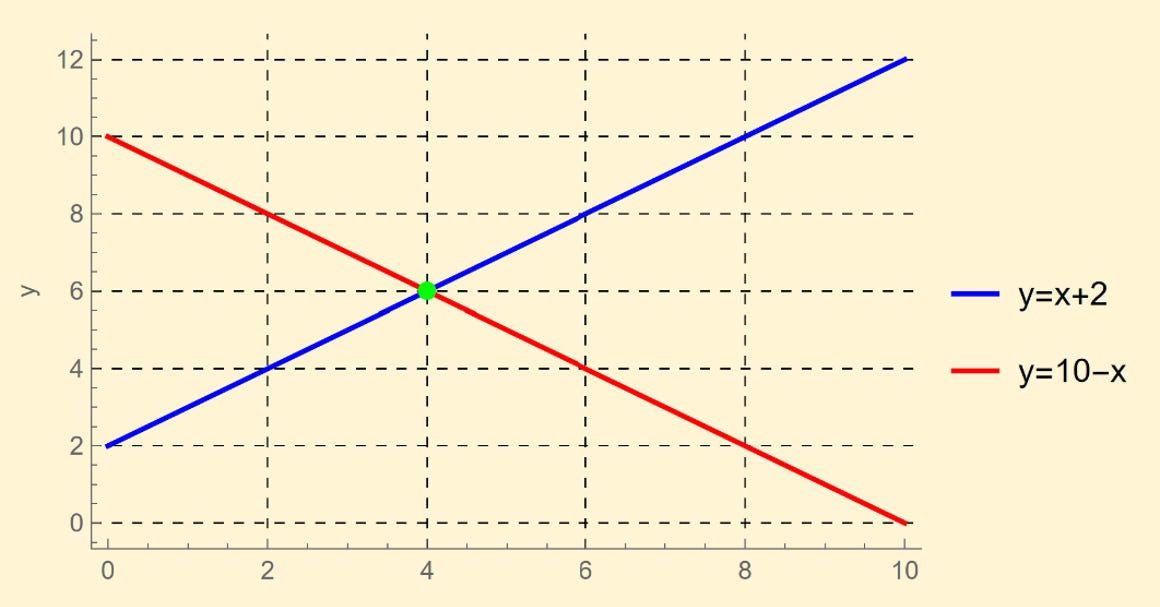
This equation
produces the line in this plot
It just means you take whatever number you see on the horizontal axis and add 2 to get the corresponding number on the vertical axis.
This equation
produces this plot
Here you just start with 10 and subtract whatever is on the x axis to get what is on the y axis. In both cases, y is related to x in an uncomplicated, linear way. Life is simple. Below you put them together and they meet at the green dot
The foregoing, although intimidating to some and terrifying to journalism majors, is pretty easy stuff. Just following the intersections of the dashed lines with no mathematical training whatsoever tells the story.
I am not making this up
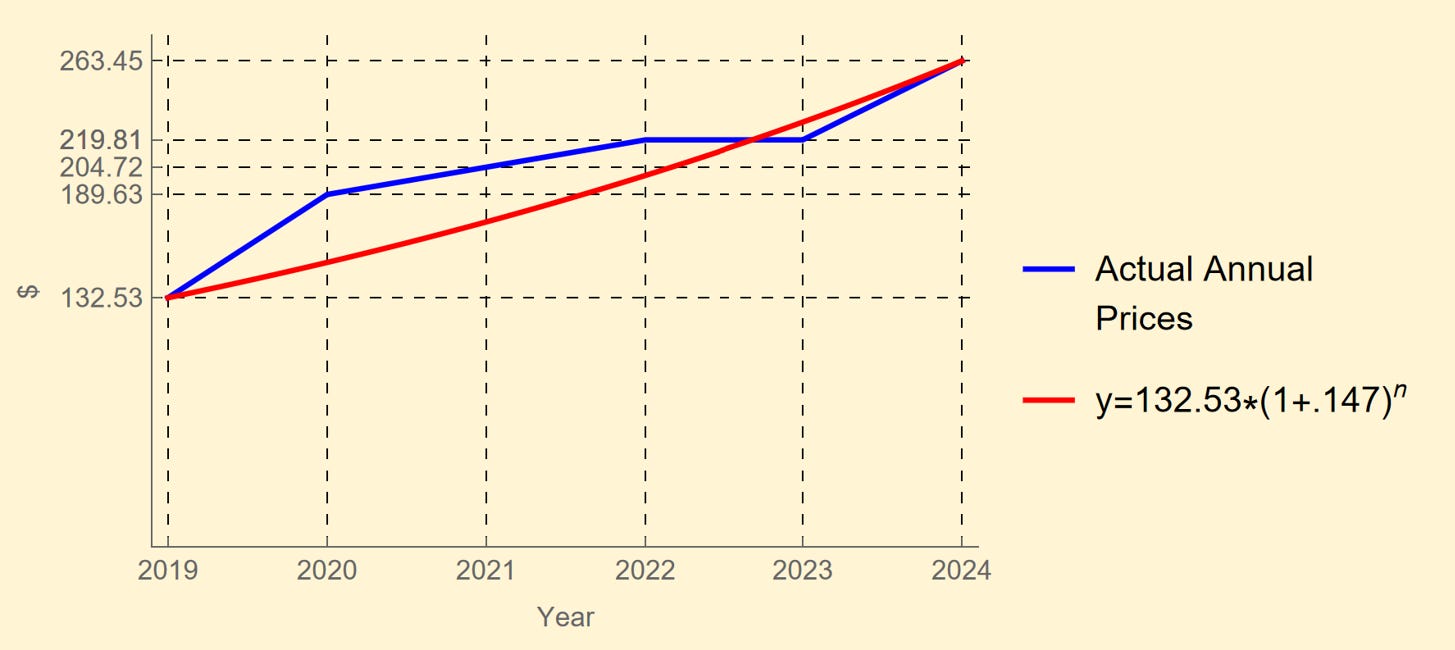
I own a plumbing fixture that requires a filter which has a useful life of one year. When I replaced it the first time in 2019, I paid $132.53. Last month I paid $263.45 for the 6th replacement. The equation is now something the calculator in your cell phone may not do which is solve for r here:
132.53*(1+r)5=263.45
But fear not, your Uncle Roger (and the AI bot in your Chrome browser - try it!!) can. Now y is “$” and x is n which stands for each “year” (numbered 1 through 5) on the plot. This is one way to calculate the inflation of the price of a single item over time.
What Jerome Powell (and YOU) should be worried about
In the plot below we stretch out time to make n very large. Remember when we were saving money to buy charcoal 16 years from now? I better start saving, because at the rate it has been rising, that filter will cost me $2,723.95 in the year 2040. Your children will pay more, passing through $10,000 a few years after. It is uncertain whether your grand-children will see the cost of that filter approach $40,000. Usually societies collapse before that. Who was elected in 2024 will be irrelevant then.
Returning to my most recent plumbing filter prices, the alert reader may have noticed that I took some liberties with the computation. The equation 132.53 *(1+.147)5 = 263.45 imagines that prices increased smoothly in approximately the same increment each year. This was not the case. For instance, in two years – 2022 and 2023 – the price was the same. The jagged edges of the actual prices are shown in blue below. Note, however, that the red curve starts and stops at the same place as the jagged blue line does.
This bit of mathematical wizardry is harmless in the present context. But is this always so? Consider the case of a longer time period with smaller time increments having considerably more variation. There is a way to express the piecemeal jagged plot in blue above algebraically, via an equation as we have been doing with other examples this week. Such an equation, to say the least, would be “messy” and get worse with longer periods and more frequent, short intervals. Welcome to the world of time-dependent differential equations. This is a branch of math that has very few solutions. Needless to say (at least I hope it is needless), this is a very complex matter.
Now suppose that you have two of these ugly equations. Further, suppose you wish to predict when and at what value the two intercept. Remember the green dot above? Last week we showed just such a situation. Here it is again, where you are required to constantly monitor inflation and interest rates, where the two only intersect three times (green dots) in 16 years.
Now, just how easy do you suppose this would be? Think of everything in all the aisles in the grocery store, each having a price profile that varies over time. Thinking about interest rates again? You should be. To buy food in your retirement, between now and the day you retire you need to constantly and instantaneously offset price increases with equivalently changing investment returns.
Sounds like loads of fun.
[Next week: The tradeoff of living]