The Rubber Yardstick

(How to get any answer you want)

One Inauguration Day past, a US President (it does not matter which one) sent a memo to heads of federal agencies and departments instructing them to (I am not making this up) “…identify ways to modernize and improve the regulatory review process to promote policies that reflect new developments in scientific and economic understanding, fully account for regulatory benefits that are difficult or impossible to quantify, and does not have harmful anti-regulatory or deregulatory effects…”

Studying this delightful snippet of wonkspeak, I tried to determine its meaning. The best I have come up with so far is that the President was telling his subordinates to round up all the tall short men.

Parsing it helps a little. My favorite section is “…fully account for regulatory benefits that are difficult or impossible to quantify…” Am I the only one to see the oxymoron “regulatory benefit” or in “accounting” for something “impossible to quantify”? Nonetheless, I finally found a way to model it.

I know you will be pleased…

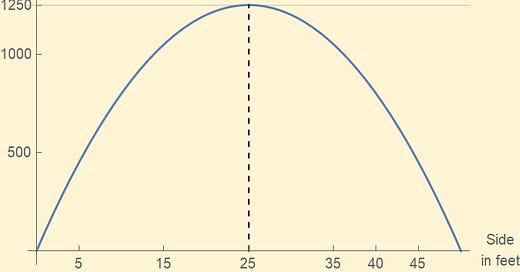
Before we reflect on “new developments in scientific and economic understanding”, we should review old standards that have stood the test of time. One of these is the concept of “optimization” which, under proper conditions, allows you to compute PRECISELY the BEST alternative. This technique has been around for hundreds of years, used successfully by millions of human beings. So, for instance, imagine the President wants to create a rectangular area immediately adjacent to the White House to keep all the tall short men his staff locates. Suppose he will use the exterior wall of the White House as one side and he has only 100 feet of fence material for the remaining three sides. He does not know how many men will need to fit into the enclosure but he wants it to be as big as possible in case there are lots of them. Thus, he has an optimization problem: He wants to maximize the area of the enclosure, subject to the fence material constraint.

There is a simple little calculus procedure (neatly described here) that tells the President to make the sides 50 feet apart, each 25 feet long. This will use all the fencing material and end up with a 1250 square foot pen. Any other combination would result in either having leftover fence (a waste of taxpayer dollars) or gaps (allowing the tall short men to get out). This approach to decision making has no “harmful anti-regulatory or deregulatory effects” for the simple reason that it is the only way it can be done. Below is a graph of all the suboptimal choices leading up to the best one where you would expect it to be, at the top.

Here is where I get into trouble for being too simplistic and too complicated at the same time. I should be careful lest I end up inside a fence somewhere.

Suppose whatever is required involves two possible optima, one better than the other. For instance, the President may want a top on the enclosure so no one can climb out. He does not know the height of the tallest of the tall short men. To have them stooped over would certainly not do. He views the height of the enclosure as a regulatory benefit that is difficult or impossible to quantify. Not necessarily. Here is a slightly harder, but possible, computation illustrating two alternative heights for the enclosure.

The dilemma is now complicated by not knowing the height of every tall short man in the country. At the “Pretty Good” level (AKA “close enough for government work”) we can accommodate men of just under 6 feet. Is it better to have it higher in case some are taller than that? Who is to decide?

This, the President leaves to his minions. It turns out that some of these government employees have favorites. They prefer tall short men with a certain amount of money, or a certain level of education. Or, they believe that some tall short men have been treated too well by life thus far and should be punished, giving precedence to those less fortunate. The people in charge of determining the height of the enclosure divide society into two groups: the Favored Class and the Others. They then count those in the Favored Class and decide accordingly. The benefit is provided as you see below, set to accommodate those in the Favored Class. The Others may have to stoop but that is just too bad.

So, when we needed only the optimum area there was no doubt. The calculation was precise and agnostic about the outcome. There was no “fair” and no favoritism to determine “fair.” But height was decided in a way so as to “promote policies that reflect” the subjective choice of whomever is making the rules. This is a widely known tradeoff in society: Do you decide how to make the Pie as big as possible and then decide how it is to be divided; or do you decide who gets what share of the Pie before deciding how big it is to be. The latter, from each according to his abilities and to each according to his need, invariably produces a smaller pie and all of society is worse off as a result.

When decisions are made by all the King’s horses and all the King’s men, measurement is corrupted. All is subjective. There is no objective measure of anything. The yardstick is made of rubber. Whatever measure the King wants is possible. Thus:

Extra Credit: What happens after a peaceful transfer of power? The short answer is “Not much” (recall it does not matter which President). The pendulum swings back and forth as two chummy parties pass the plate between them in alternate seasons. The new potentate merely rearranges the height of the lid on the pen temporarily to conform to his favored class.

One thing you may be sure of, the Ruling Political Class will be selling the fencing material. Their share is collected first. Always.